Introduction
At Hunters we aim to detect threat actors hiding in our customers’ assets. In order to do so, Hunters XDR autonomously analyzes security logs to search for various types of information: IOCs from threat intel feeds, signatures of malicious behavior based on a variety of TTPs, or anomalies in the data that could potentially indicate that an attacker is trying to hide their activity, among others. To accomplish this, Hunters’ Artificial Intelligence team constantly researches and solves complex ML problems, and leads the implementation of ML algorithms that enable autonomous detection and analytics.
Our goal throughout this post is to elaborate on how we use SHAP values to explain Hunters models’ prediction in order to increase threat detection accuracy and expedite response time. Specifically, this post will dive into a segment of how Hunters’ solution performs anomaly detection: it detects anomalies or deviations from an observed behavior, in order to understand whether that anomalousness can be correlated with maliciousness.
Machine learning-based detection solutions such as Hunters XDR must provide a clear explanation when the model alerts on an interesting event. Providing such explanation is critical for increasing the confidence of the security analysts in the model, as it enables them to:
- Review the detected incident and understand the anomalous properties associated with it to assess its validity and severity.
- Better investigate the event by understanding the root cause of an alert.
Consider, for instance, a model that detects anomalous logins. A security analyst would want to be able to understand what properties of the login caused the model to mark it as anomalous: Was it the IP address? Was it the user agent, or maybe the unusual hour of the login? Knowing the anomalous properties that led the model to alert on a signal promotes faster decision making. It also enables refinement and improvement of the model.
What is SHAP
Explaining a model’s prediction can be a difficult task. This is especially true for models that use ensemble methods, i.e combining the results of many independent base learning models.
SHAP ( SHapley Additive exPlanations ) is a method of assigning each feature a value that marks its importance in a specific prediction. As the name suggests, the SHAP algorithm uses Shapley values. The Shapley value is a concept developed by Lloyd Shapley in 1951 in the game theory field, in which the setup is described as following: A group of players are playing a game and receive some rewards as the result of it. How should we distribute the rewards between all the players?
In their papers, Lundberg and Lee (authors of the first paper on SHAP – “A Unified Approach to Interpreting Model Predictions”) suggest to apply the Shapley theorem in order to explain machine learning predictions. In the machine learning setting we have many features (players) and each of them contributes a different amount to the final prediction. Our goal is to understand how much of the prediction each feature is responsible for.
There are some properties that we want the rewards’ distribution to hold:
- Efficiency: We want to distribute all the rewards, so the sum of all the Shapley values should be equal to the total amount.
- Symmetry: If two players contribute the same, then their rewards should be the same too. In our setup we can think about it as if one feature can be replaced with another feature, and would have still gotten the same prediction, then the importance of the two features is the same.
- Null player: The Shapley value for a player that is contributing zero to the reward should be zero. In our case such a player is a feature that doesn’t change the prediction.
- Linearity: If the same group plays two games then each player’s rewards from both games should be equal to the sum of the reward from the first game and second game.
It turns out that there is only one way to compute values that will hold those properties: the value is the average of the marginal contributions of the feature. As a result, we have to compute the marginal contribution for each possible set of features. It is worth noting that in many models that aren’t linear we will also need to iterate on all the possible orders of features and not only the combinations, since the order can change the contribution of each feature.
Simply put, we can use Shapley values to calculate each feature’s contribution to the prediction by computing its marginal contribution for each possible set of features. For each subset of features we compute the reward function with the specific player and subtract the reward without this player. Then we normalize it by the number of possible player subsets.
SHAP Value For Trees
Computing the SHAP values in the general case can be very hard to do in an efficient manner, since we need to iterate over all the possible subsets of features, especially if we need to take the order of the features into account. In their paper, Lundberg and Lee described some optimization methods to compute the SHAP values faster specifically for tree-based models.
Some families of machine learning algorithms have an ensemble of trees (also called Forest), and each internal node in the tree splits the data according to some feature. In order to predict the value of some specific point, we will go down the tree by the splitting of the feature in the nodes. Then we usually average the results from all the trees in the ensemble to get the final model prediction (as results can vary greatly between trees). Two popular such models are Random Forest for classification and regression problems and Isolation Forest for anomaly detection problems.
In our context of predicting whether a login event is malicious or benign, a simplified decision tree could look like this:
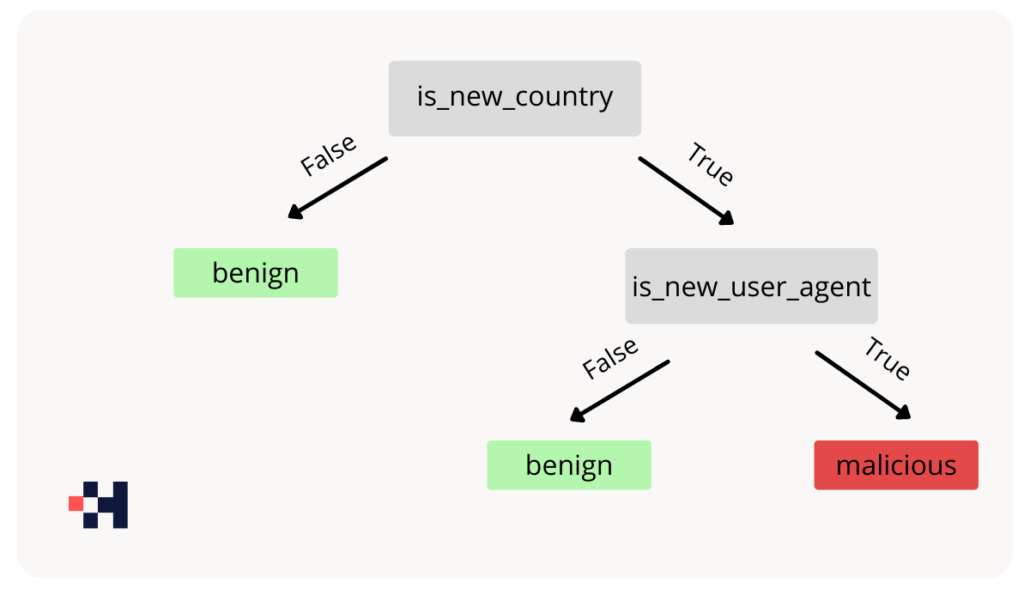
In this example, the tree will analyze some of the event’s features (such as from which country it was, or from which user agent the event took place), and finally label the event as malicious only if both the country and the user agent are new. By combining many such trees that were trained on different subsets of the data we can achieve an accurate model without overfitting.
Because of the linear properties of the Shapley values, we can calculate the value for each tree separately and then average all individual tree SHAP values to get the final SHAP values. In order to calculate SHAP for a subset of the features, on one tree, we have a simple recursive algorithm. We will traverse the tree from the leaves to the root and save the SHAP value for all internal nodes. On a leaf node, the SHAP value is equal to the value of the leaf. For each internal node, the value will be calculated from its child nodes. If the node isn’t splitting the data by a feature in our feature subset, the SHAP value of the node will be the average of its children. Otherwise, we will take the SHAP value of the child node that corresponds to the feature value. To optimize it even further, we can run a slightly modified version of this algorithm on all the possible feature subsets simultaneously.
For the example above, to calculate the SHAP value for the feature “is_new_country”, we will first calculate the values for the leaves’ nodes. For the node that was split by the “is_new_user_agent” feature, the value will be the average of its child nodes since it isn’t included in our current feature subset.
SHAP Explainability
There are two key benefits derived from the SHAP values: local explainability and global explainability.
For local explainability, we can compute the SHAP values for each prediction and see the contribution of each feature. Let’s imagine a simplified model for detection of anomalous logins. The model uses the following features: the country of the source IP address, the MFA method used, the browser, and the operating system extracted from the user agent. When a login is marked as anomalous, we can show the analyst if the anomalous part of the login was related to the IP address or to the MFA method. Note that in this example, the more anomalous the login, the lower the score the model assigns to it.
In the example, the user usually logs in from England using a YubiKey.
On a normal login, all of our features have a positive contribution to the score.

As we can see, each feature increased the output of the model and marked the event as less anomalous.
But in case of an attack where someone stole the user’s password and passed the MFA using SMS hijacking, we can highlight for the analyst the suspicious properties of the event.

And as we can see, the MFA method and the country marked the event as more anomalous while the OS and browser are not anomalous because those are common values for this user.
Another important benefit of SHAP values is global explainability. We can aggregate all the local explanations to better understand the impact of specific features on the entire model and the correlation between the features. By aggregating all the SHAP values of all the samples, we can see which features contribute most in average, and towards which label. Additionally, we can look at the correlation between the SHAP value of one feature and another.
We saw that it is important to have the ability to explain and interpret machine learning models in order to make their prediction more transparent, and more actionable. It isn’t enough to know that certain events are interesting but rather we want to know why they are. We saw that by leveraging Shapley and SHAP values we can calculate the contribution of each feature and see why the model predicted its prediction.
Equipped with the model’s explanation, the analyst can understand better and faster the root cause of a security alert presented by the machine, and by highlighting the suspicious entity in the event we can focus on the entities most relevant to the detection, and correlate them with other relevant events.




